近日，中國科學(xué)院重慶綠色智能技術(shù)研究院自動(dòng)推理與認知團隊在數值求解參數非線(xiàn)性系統研究中取得進(jìn)展，率先提出了運用關(guān)鍵點(diǎn)集、同倫方法和數值投影求得參數多項式系統的邊界曲線(xiàn)和參數動(dòng)力系統的分叉曲線(xiàn)。該方法突破了傳統數值方法的局部性限制，可以給出參數空間的完整劃分，對研究非線(xiàn)性系統的穩定性具有十分重要的意義。相關(guān)成果在符號數值混合計算的重要會(huì )議“International Workshop on Computer Algebra in Scientific Computing ”及“International Symposium on Symbolic and Numeric Algorithms for Scientific Computing”上作了報告。其中“A Numerical Method for Computing BorderCurves of Bi-parametric Real PolynomialSystems and Applications”一文已在線(xiàn)發(fā)表。另一篇文章“A Numerical Method for Analyzing the Stability ofBi-parametric Biological Systems”已被接收，將于2017年上半年發(fā)表。 

　　參數多項式系統廣泛存在于機器人控制、生物化學(xué)系統穩定性分析、程序的優(yōu)化和驗證等眾多應用領(lǐng)域。參數多項式系統解的結構十分復雜，對不同的參數值，系統可以無(wú)解、只有有限個(gè)解或者無(wú)窮多個(gè)解，無(wú)窮多個(gè)解的情況又可以有不同的維數。符號計算方法理論上可以得到參數空間的完整劃分，但實(shí)際計算中會(huì )產(chǎn)生中間表達式膨脹。傳統的數值方法依靠仿真或局部曲線(xiàn)追蹤通常只能得到部分的邊界曲線(xiàn)。自動(dòng)推理與認知中心吳文淵和陳長(cháng)波提出在某些假設條件下可以通過(guò)追蹤高維空間曲線(xiàn)的所有連通分支和數值投影來(lái)得到參數空間的邊界曲線(xiàn)。這一方法可以將參數多項式系統的求解分為離線(xiàn)和在線(xiàn)兩部分。在線(xiàn)部分通過(guò)構造實(shí)同倫有望實(shí)時(shí)求解參數多項式系統，具有很大的應用潛力。上述研究成功將這一方法應用于生物系統的穩定性分析中。該研究成果作為自動(dòng)推理與認知中心零誤差計算研究方向的最新進(jìn)展，主要面向工程應用，得到國際同行的高度評價(jià)。

　　上述研究?jì)热莴@得國家自然科學(xué)研究基金及中科院前沿科學(xué)重點(diǎn)研究項目支持。 

　　

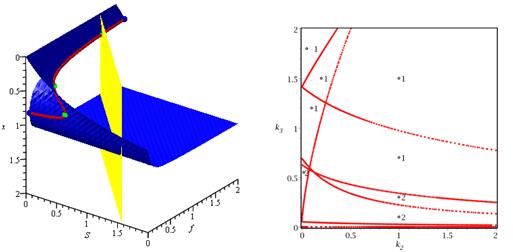
　　算法幾何描述及分叉邊界及穩定點(diǎn)個(gè)數分布