光電所先進(jìn)光學(xué)研制中心吳永前課題組在隨機相移技術(shù)研究上取得新進(jìn)展：首先提出了一種基于Lissajous圖形和橢圓擬合技術(shù)的相位提取誤差標定方法，該方法適用于任意相移算法的隨機相移誤差標定；并成功擴展為完全隨機相移算法。該算法在高精度動(dòng)態(tài)干涉測量領(lǐng)域有很大的潛在應用價(jià)值。相關(guān)研究結果分別發(fā)表于Optics Express與近期的Optics and Lasers in Engineering 。 

　　相移誤差，尤其是由于機械振動(dòng)造成的隨機相移誤差一直是高精度相移干涉測量的最大誤差源之一，它直接導致由傳統相移算法解算出的面形帶有二倍條紋頻率的“波紋”誤差。針對相移器的線(xiàn)性及非線(xiàn)性造成的靜態(tài)相移誤差，已有眾多研究并發(fā)展出了相應的免疫算法；但對于外界振動(dòng)導致的動(dòng)態(tài)隨機相移誤差，現有的研究重點(diǎn)主要集中于通過(guò)各種方法（迭代、非迭代）計算出每幀干涉圖的隨機相移誤差大小然后進(jìn)行相應補償，過(guò)程一般較為耗時(shí)且計算精度不高。 

　　針對相移算法中的相位提取函數一般是反正切函數的特性，本研究把相位提取函數的分子項和分母項看成一對頻率相同，相位差大約是的二維簡(jiǎn)諧振動(dòng)，通過(guò)做Lissajous圖形和曲線(xiàn)擬合得到Lissajous橢圓的參數表達式。最后通過(guò)Lissajous橢圓（存在相位提取誤差）到單位圓（沒(méi)有相位提取誤差）的參數轉變過(guò)程（ellipse to circle, ETC）實(shí)現相位提取誤差的標定。本標定方法不需要計算每幀干涉圖的真實(shí)相移量，只需要一次橢圓擬合和ETC運算，具有簡(jiǎn)單，高效，通用性強等優(yōu)點(diǎn)，對隨機相移技術(shù)的研究具有重要價(jià)值。 

　　通過(guò)對先進(jìn)迭代算法（AIA）的研究，ETC成功擴展為ETC iterative（ETCI）算法。該算法是一種完全意義上的隨機相移算法，只需要三步左右迭代便可從一系列隨機相移的干涉圖中高精度恢復出相位面形信息，并且不存在相位符號翻轉問(wèn)題。通過(guò)算法優(yōu)化并借助GPU，FPGA等并行計算硬件平臺，本算法有望實(shí)現高精度實(shí)時(shí)動(dòng)態(tài)測量。 

　　

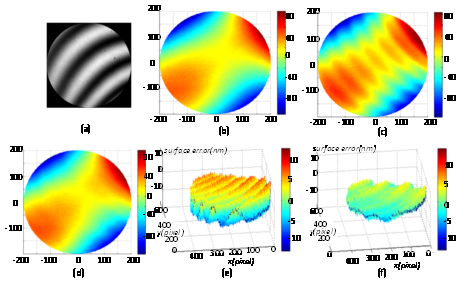
　　圖1 實(shí)驗中振動(dòng)對面形（較大像散）的影響與ETC校正后的面形 

　　

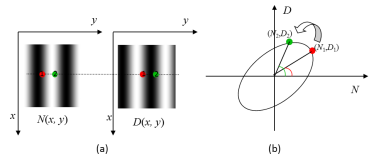
　　圖 2 由相位提取函數的分子項與分母項所做的Lissajous 圖及相位符號判斷 

　　

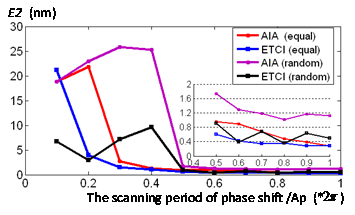
　　圖 3 ETCI與AIA在不同相移情況下的計算精度對比